Abstract: Huffman coding has been used as a coding method in life. In the following, we use Huffman coding and decoding implemented in Java as the core to describe its coding method and program.
Huffman coding definitionHuffman Coding, also known as Huffman coding, is a coding method. Huffman coding is a type of variable word length coding (VLC). In 1952, Huffman proposed an encoding method that constructs the codeword with the shortest average length of the heterograph head based on the probability of occurrence of characters, sometimes called the optimal encoding, which is generally called Huffman encoding (sometimes called Hoff). Man coding).
Huffman coding principle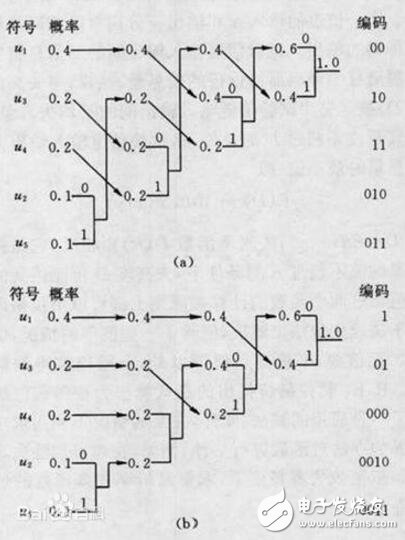
Let a source generate five symbols u1, u2, u3, u4 and u5, corresponding probability P1 = 0.4, P2 = 0.1, P3 = P4 = 0.2, P5 = 0.1. First, the symbols are queued by probability from large to small, as shown. When encoding, starting with two symbols of minimum probability, one of the branches can be selected as 0 and the other branch is 1. Here, we choose the branch to be 0 and the lower branch to be 1. The probabilities of the encoded two branches are then combined and re-queued. Repeat the above method multiple times until the merge probability is normalized. It can be seen from Figures (a) and (b) that although the average code lengths are equal, the same symbol can have different code lengths, that is, the encoding method is not unique, because the two paths are combined and re-queued. There may be several branches with equal probability, which makes the queuing method not unique. In general, if the newly merged branch is discharged to the uppermost branch of the equal probability, it will be advantageous to shorten the code length variance, and the coded code is closer to the equal length code. Here, the coding of (a) is better than (b).
The codeword of the Huffman code (the code of each symbol) is an isopreamble code, that is, any codeword will not be the front part of another codeword, which allows each codeword to be transmitted together without intermediate In addition to the isolation symbol, as long as the transmission does not go wrong, the receiver can still separate the codewords, so as not to be confused.
In practical applications, in addition to using timing cleaning to eliminate error diffusion and buffer storage to solve rate matching, the main problem is to solve statistical matching of small symbol sets, such as black (1), white (0) fax source statistical matching, The extended symbol set source is composed of 0 and 1 different length runs. Run, refers to the length of the same symbol (such as the length or number of consecutive 0 or a string 1 in the binary code). According to the CCITT standard, it is necessary to count 2 & TImes; 1728 kinds of runs (length), so that the amount of storage at the time of implementation is too large. In fact, the probability of a long run is small, so CCITT also stipulates that if l represents the length of the run, then l=64q+r. Where q is the primary code and r is the base code. When encoding, the run length of not less than 64 is composed of a primary code and a base code. When l is an integer multiple of 64, only the code of the main code is used, and the code of the base code does not exist.
The main code and the base code of the long run are encoded by the Huffman rule. This is called the modified Huffman code, and the result is available. This method has been widely used in document fax machines.
Java implements Huffman encoding and decodingHuffman encoding is performed on a character string; in the encoding process, the encoding of each character is obtained, and the previous encoding is decoded by the encoding of each character known.
Analysis: The first is the Huffman coding algorithm, which refers to the description of the Huffman coding algorithm in Li Zeian's "Multimedia Technology Tutorial":
• IniTIalizaTIon: Put all symbols on a list sorted according to their frequency counts.
•Repeat unTIl the list has only one symbol left:
-From the list pick two symbols with the lowest frequency counts. Form a Huffman subtree that has these two symbols as child nodes and create a parent node.
-Assign the sum of the children's frequency counts to the parent and insert it into the list such that the order is maintained.
–Delete the children from the list.
•Assign a code word for each leaf based on the path from the root.
My code is implemented based on this algorithm description. In fact, I read the Chinese version, but I did not find the Chinese electronic version of the book, so I had to stick the English version. However, fortunately, the English version is not complicated.
Next is decoding. Although the decoding process is simple, it is the reason for this article. I read some articles on the Internet and ignored one question: What are the things in the encoding and decoding process? That is, rely on what to decode? The answer to this article is "encoding of each character", which is generated during the encoding process and passed along with the string encoding to the decoder for decoding. You can also say "the number of times each character appears" or "Huffman Tree", whether it is "the number of times each character appears" or "Huffman Tree", you need to get "each character through them" Encoding can only be done after decoding.
Here is the Java code:
[java] view plain copypackage com.liyuncong.algorithms.algorithms_huffman;
/**
* Huffman tree nodes
* @author yuncong
*
*/
Public class Node implements Comparable "Node" {
Private Node leftChild = null;
Private Data data = null;
Private Node rightChild = null;
Public Node getLeftChild() {
Return leftChild;
}
Public void setLeftChild(Node leftChild) {
this.leftChild = leftChild;
}
Public Data getData() {
Return data;
}
Public void setData(Data data) {
This.data = data;
}
Public Node getRightChild() {
Return rightChild;
}
Public void setRightChild(Node rightChild) {
this.rightChild = rightChild;
}
@Override
Public String toString() {
Return "Node [leftChild=" + leftChild + ", data=" + data
+ ", rightChild=" + rightChild + "]";
}
@Override
Public int compareTo(Node o) {
Return this.data.compareTo(o.getData());
}
}
[java] view plain copypackage com.liyuncong.algorithms.algorithms_huffman;
/**
* Data is used to store a character and the number of occurrences
* @author yuncong
*
*/
Public class Data implements Comparable《Data》{
// character
Private char c = 0;
// The number of occurrences of the character
Private int frequency = 0;
Public char getC() {
Return c;
}
Public void setC(char c) {
This.c = c;
}
Public int getFrequency() {
Return frequency;
}
Public void setFrequency(int frequency) {
This.frequency = frequency;
}
@Override
Public String toString() {
Return "Data [c=" + c + ", frequency=" + frequency + "]";
}
@Override
Public int compareTo(Data o) {
If (this.frequency " o.getFrequency()) {
Return -1;
} else if (this.frequency 》 o.getFrequency()) {
Return 1;
} else {
Return 0;
}
}
}
[java] view plain copypackage com.liyuncong.algorithms.algorithms_huffman;
Import java.util.Map;
/**
* The result of encoding the string: including the encoded string and the character/encoding pair
* @author yuncong
*
*/
Public class EncodeResult {
// string encoded result
Private String encode;
// character encoding pair
Private Map "Character, String" letterCode;
Public EncodeResult(String encode, Map "Character, String" letterCode) {
Super();
This.encode = encode;
this.letterCode = letterCode;
}
Public String getEncode() {
Return encode;
}
Public Map "Character, String" getLetterCode() {
Return letterCode;
}
}
[java] view plain copypackage com.liyuncong.algorithms.algorithms_huffman;
Public interface HuffmanAlgorithm {
/**
* Encoded strings.
* @param str specified string to be encoded
* @return encoding result
*/
Public EncodeResult encode(String str);
/**
* Returns the original string based on the encoding result.
* @param decodeResult The result of encoding the original string.
* @return The decoded string.
*/
Public String decode(EncodeResult encodeResult);
}
[java] view plain copypackage com.liyuncong.algorithms.algorithms_huffman;
Import java.util.ArrayList;
Import java.util.HashMap;
Import java.util.Map;
Import java.util.Set;
Import com.liyuncong.application.commontools.FileTools;
Public abstract class HuffmanAlgorithmAbstract implements HuffmanAlgorithm {
@Override
Public EncodeResult encode(String str) {
ArrayList "Node" letterList = toList(str);
Node rootNode = createTree(letterList);
Map "Character, String" letterCode = getLetterCode(rootNode);
EncodeResult result = encode(letterCode, str);
Return result;
}
/**
* Convert a string to a list of nodes
* @param letters
* @return
*/
Private ArrayList "Node" toList(String letters) {
ArrayList "Node" letterList = new ArrayList "Node" ();
Map "Character, Integer" ci = new HashMap "Character, Integer" ();
For (int i = 0; i " letters.length(); i++) {
Character character = letters.charAt(i);
If (!ci.keySet().contains(character)) {
Ci.put(character, 1);
} else {
Integer oldValue = ci.get(character);
Ci.put(character, oldValue + 1);
}
}
Set "Character" keys = ci.keySet();
For (Character key : keys) {
Node node = new Node();
Data data = new Data();
data.setC(key);
data.setFrequency(ci.get(key));
node.setData(data);
letterList.add(node);
}
Return letterList;
}
Protected abstract Node createTree(ArrayList "Node" letterList);
/**
* Encoded strings.
* @param letterCode Character/code pair set.
* @param letters specifies the string to be encoded.
* @return encoding result
*/
Private EncodeResult encode(Map "Character, String" letterCode, String letters) {
StringBuilder encode = new StringBuilder();
For (int i = 0, length = letters.length(); i "length; i++) {
Character character = letters.charAt(i);
Encode.append(letterCode.get(character));
}
EncodeResult result = new EncodeResult(encode.toString(), letterCode);
Return result;
}
/**
* Get all character encoding pairs
*
* @param rootNode Huffman tree root node
* @return all character encoding pairs
*/
Private Map "Character, String" getLetterCode(Node rootNode) {
Map "Character, String" letterCode = new HashMap "Character, String" ();
/ / Deal with only one node
If (rootNode.getLeftChild() == null && rootNode.getRightChild() == null) {
letterCode.put(rootNode.getData().getC(), "1");
Return letterCode;
}
getLetterCode(rootNode, "", letterCode);
Return letterCode;
}
/**
* Randomly traverse the Huffman tree to get all character encoding pairs.
*
* @param rooNode Huffman tree root node
* @param suffix encoding prefix, which is all encoding on the previous path when encoding this character
* @param letterCode is used to save character encoding results
*/
Private void getLetterCode(Node rooNode, String suffix,
Map "Character, String" letterCode) {
If (rooNode != null) {
If (rooNode.getLeftChild() == null
&& rooNode.getRightChild() == null) {
Character character = rooNode.getData().getC();
letterCode.put(character, suffix);
}
getLetterCode(rooNode.getLeftChild(), suffix + "0", letterCode);
getLetterCode(rooNode.getRightChild(), suffix + "1", letterCode);
}
}
Public String decode(EncodeResult decodeResult) {
// decoded string
StringBuffer decodeStr = new StringBuffer();
// Get the decoder
Map "String, Character" decodeMap = getDecoder(decodeResult
.getLetterCode());
// decoder key set
Set "String" keys = decodeMap.keySet();
// the (encoded) string to be decoded
String encode = decodeResult.getEncode();
// The reason why the match is successful from the shortest is because of the unique prefix nature of Huffman coding.
// Temporary possible key values
String temp = "";
/ / Change the size of the temp cursor
Int i = 1;
While (encode.length() 》 0) {
Temp = encode.substring(0, i);
If (keys.contains(temp)) {
Character character = decodeMap.get(temp);
decodeStr.append(character);
Encode = encode.substring(i);
i = 1;
} else {
i++;
}
}
Return decodeStr.toString();
}
/**
* Obtain the decoder, that is, get the encoding/character pair by letter/encoding pair.
*
* @param letterCode
* @return
*/
Private Map "String, Character" getDecoder(Map "Character, String" letterCode) {
Map "String, Character" decodeMap = new HashMap "String, Character" ();
Set "Character" keys = letterCode.keySet();
For (Character key : keys) {
String value = letterCode.get(key);
decodeMap.put(value, key);
}
Return decodeMap;
}
}
[java] view plain copypackage com.liyuncong.algorithms.algorithms_huffman;
Import java.util.ArrayList;
Import java.util.HashMap;
Import java.util.Map;
Import java.util.Set;
/**
* Algorithm implementation reference "Multimedia Technology Tutorial"
* @author yuncong
*
*/
Public class HuffmanAlgorithmImpl1 extends HuffmanAlgorithmAbstract {
/*
* Create a Huffman tree; Lose the data in the letterList, the deep copy of the letterList is a perfect place
*/
@Override
Protected Node createTree(ArrayList"Node" letterList) {
Init(letterList);
While (letterList.size() != 1) {
Int size = letterList.size();
// The small node is placed on the right (left side of the eye)
Node nodeLeft = letterList.get(size - 1);
Node nodeRight = letterList.get(size - 2);
Node nodeParent = new Node();
nodeParent.setLeftChild(nodeLeft);
nodeParent.setRightChild(nodeRight);
Data data = new Data();
data.setFrequency(nodeRight.getData().getFrequency()
+ nodeLeft.getData().getFrequency());
nodeParent.setData(data);
letterList.set(size - 2, nodeParent);
letterList.remove(size - 1);
Sort(letterList);
}
Node rootNode = letterList.get(0);
Return rootNode;
}
/**
* Initialization makes the list of nodes order
*/
Private void init(ArrayList"Node" letterList) {
Sort(letterList);
}
/**
* Bubble sorting, putting small at the end
*/
Private void sort(ArrayList"Node" letterList) {
Int size = letterList.size();
/ / Deal with only one element, that is, do not need to sort
If (size == 1) {
Return;
}
For (int i = 0; i " size; i++) {
For (int j = 0; j " size - 1 - i; j++) {
If (letterList.get(j).getData().getFrequency() " letterList
.get(j + 1).getData().getFrequency()) {
Node tempNode = letterList.get(j);
letterList.set(j, letterList.get(j + 1));
letterList.set(j + 1, tempNode);
}
}
}
}
}
[java] view plain copypackage com.liyuncong.algorithms.algorithms_huffman;
Import static org.junit.Assert.*;
Import org.junit.Test;
Public class HuffmanAlgorithmImpl1Test {
@Test
Public void testEncodeString() {
HuffmanAlgorithmImpl1 huffmanImpl1 = new HuffmanAlgorithmImpl1();
EncodeResult result = huffmanImpl1.encode("abcdda");
System.out.println(result.getEncode());
}
@Test
Public void testDecode() {
HuffmanAlgorithmImpl1 huffmanImpl1 = new HuffmanAlgorithmImpl1();
EncodeResult result = huffmanImpl1.encode("abcdda");
String decode = huffmanImpl1.decode(result);
System.out.println(decode);
}
}
Toggle Switches,Waterproof Toggle Switch,Waterproof Rocker Switch,Mini Toggle Switch
Lishui Trimone Electrical Technology Co., Ltd , https://www.3gracegfci.com
