
As artificial intelligence systems play an increasingly important role in the real world, understanding how different systems interact is critical.
Just now, DeepMind published a paper called Symmetric Decomposition of Asymmetric Games. In this paper, DeepMind researchers used a branch of game theory to try this problem.
The researchers focused on how the two agents will behave and behave in an asymmetric game such as Texas Hold'em and board games.
With this new approach, the agent can find Nash equilibrium simply and quickly in a complex asymmetric game.
Game and Nash Equilibrium
Game theory is a branch of mathematics that is used to analyze the strategies of decision makers in a competitive environment.
This set of theories applies to humans, animals, and multiple AI environments with more than one AI. For example, multiple robots in the house clean the room at the same time.
The asymmetric information game simulates real-world scenarios, just as the mindset and motivation of buyers and sellers are different at auction. The results we get give us our own insights and analyze them in an extremely simple way.
The characteristics of asymmetric games are that each player has different strategies, goals and rewards. For example, the most common coordination game in game theory research, the war of gender.
In general, the evolutionary dynamics of a multi-AI system is analyzed by a simple symmetric game. For example, the classic prisoner's dilemma, both players can take the same action. Even though these games can provide effective insights for multiple AI systems, telling us how to operate all players to get the best results (this is Nash Equilibrium), they can't simulate everything.
DeepMind's new approach can quickly and easily find Nash equilibrium in complex asymmetric games.
Although the current focus of this theory is still applied to the interaction of multiple AI systems, researchers believe that this conclusion can also be used in economics, evolutionary biology, and empirical game theory.
Opera or movie?
Let me give you an example.
Two players need to decide whether to go to the opera or the movie at night. Unfortunately, one of them prefers opera and the other prefers movies. This is an asymmetrical game, although two players can choose any one, but depending on the player's preference, each player gets a different reward.
However, in order to maintain their friendship, or we call it a balance, both parties need to choose the same activity, so the return on individual action is zero.

The game has three balances: (i) both sides go to the opera, (ii) both parties go to the movies, and (iii) there is a blending option where each player chooses the option they like in three-fifths of the time.
The last option for this "unstable" is to use a method that simplifies or decomposes an asymmetrical game into its symmetric peer.
We can imagine the essence of this game as that each player's bonus score table is an independent symmetrical two-player game with a balance point that is consistent with the original asymmetrical game.
In the image below, the Nash Equilibrium is obtained through two peers, helping us to quickly determine the optimal strategy in the asymmetry game (a). Conversely, an asymmetric game is used to determine the equilibrium of symmetric peers.
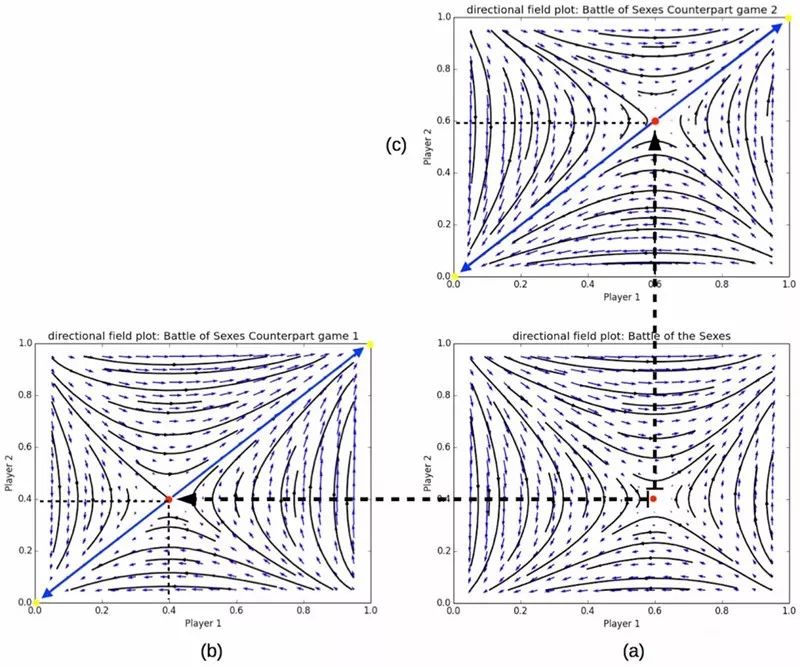
â–³ Red dot represents Nash equilibrium. For the asymmetrical game (a), the Nash equilibrium can be easily obtained from the two symmetry diagrams (b) and (c). In the above figure, the x and y axes are the probability of selecting the opera for players 1 and 2 respectively.
The good news is that this method is also suitable for other games, such as Leduc Poker. These methods apply a simple mathematical principle to quickly and directly analyze asymmetric games. We hope it will also help us understand the various dynamic systems, including multi-agent environments.
Tabbing Ribbon Machine,Photovoltaic Ribbon Welding Machine,Pv Ribbon Interconnect Machine,Ribbon High Speed Tinning Making Machine
Jiangsu Lanhui Intelligent Equipment Technology Co., Ltd , https://www.lanhuisolar.com
